We found in chapter 13 how magnification in the telescope is brought about. But this is not the only function of a telescope when used astronomically; depending on the uses to which an instrument is put, resolving power and light-gathering power may be of considerably more importance. A knowledge of some of the optical principles associated with these functions will enable the amateur to operate his own telescope to best advantage. The discussion here is necessarily brief, and may be supplemented by reference to various books listed in the bibliography.
Magnifying power has already been discussed, but in what follows it will become evident that light-gathering power and resolving power often limit the magnification which may be usefully employed. Magnifying power is otherwise independent, however, of the diameter of the objective lens or primary mirror, whereas resolving power improves as the aperture is increased and light grasp increases with the square of the aperture. The condition of the atmosphere through which we must study the sky is often the most serious factor in limiting resolution and magnification.
For visual work, the eye itself functions as the last optical system through which the light passes, the lens of the eye focusing the incoming light on the retina, which is situated at the back of the eyeball. In bright daylight, the iris of the eye contracts to a diameter of about 2 mm., and in darkness expands to 8 mm. or more; the iris thus acts as a stop in regulating the amount of light that is allowed to enter. The retina is composed of thousands of microscopic nerve endings, known as cones and rods. The cones are located near the central part of the retina, their greatest concentration being in a spot called the fovea. Acute vision is centered on the fovea, and is confined to a field of less than 1°. It is difficult to realize that this field is so small because the eye is unceasingly roving about,
picking up and discarding one object after another. Extra-foveal vision, in which the rods are chiefly engaged, may extend up to 130° or more. The rods are much more sensitive to low levels of illumination than are the cones, but as much as half an hour in complete darkness may be required to adapt them totally for night vision. Because of the location of the rods on the retina, faint objects are most readily found with averted vision, or “out of the corner of the eye.” If the object is sufficiently faint, any attempt to focus its image onto the fovea for careful scrutiny will actually result in its disappearance.
The stimulus caused by the light which passes into the eye is imparted to the cones or rods and interpreted by the brain as a picture of the object. As these nerve fibers are not in contact with one another, but are slightly separated, the picture that is seen actually consists of a multitude of adjacent areas. The size and central separation of these areas depends, in general, on the size and distribution of the fibers, much in the same way that resolution of detail in a photograph is limited by the graininess of the film.
In the focal plane of the telescope the image formed by the lens or mirror also consists of a multitude of nuclei, their angular sizes determined by the diameter of the mirror and the length of the light wave under consideration. The value of aperture becomes apparent when one realizes that with increasing diameter of the objective these dots (diffraction disks) become smaller and more light is poured into each of them by the lens or mirror. Thus, the larger the telescope, the greater the amount of detail that can be seen, other factors permitting. In discussing this subject, it is usual to consider a point source of light, such as a star.
The Diffraction Image of a Star
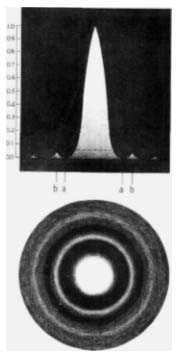
So tremendous is the distance of the stars that even such giants as Mira and Betelgeuse, whose diameters correspond approximately to that of the orbit of Mars, subtend such tiny angles (roughly 0.05 seconds of arc or less) as to be regarded as mere points. And on account of the wave nature of light, the image of a point source formed by any optical system is not itself a point, but a diffraction disk of finite size (Fig. 84), known as the Airy disk, after Sir George Airy, who in 1834 calculated the size and distribution of light in the diffraction pattern.
With a perfect optical system, about 84 per cent of the light is contained in the diffraction disk, with the other 16 per cent distributed in surrounding rings, one or two of which may be visible, depending on the brightness of the star and the stability of the atmosphere. With a mirror that is figured to within 14 wave of a paraboloid, thus performing within the Rayleigh limit (see page 76), about 68 per cent of the light is contained in the central disk; the remainder is distributed in the rings. For a quarter-wave departure from the paraboloid, doubling the Rayleigh tolerance, only about 40 per cent of the light is in the central disk, although there is no noticeable increase in its size. The lost light is deposited through the diffraction pattern, fogging up the background, so there is a loss of contrast and definition except for very brilliant objects. With further departure of the mirror’s surface from a paraboloid, there is apparent enlargement and fuzziness of the Airy disk, and definition and resolving power may become seriously impaired.
The appearance of a perfect star image as viewed in the telescope is similar to what might be seen in viewing from above a cone-shaped solid like that in Fig. 84. (The effect is simulated by inclining the page at a steep angle to the eye and squinting down the cone.) The illumination is most intense at the tip, gradually diminishing down the sides of the cone, coming to a minimum at the base aa, then rising to a second maximum, bb, to form the first bright ring. The linear diameter in the focal plane of the first minimum (aa) or of the theoretical disk containing about 84 per cent of the total light, is:
d = 1.22 y F/r,
where y is the wave length of light (0.000022″), F is the focal length, and r is the radius of the mirror.
It is thus seen that the linear size of the theoretical disk varies with the focal ratio. But since the eye, in the presence of the intense illumination at the center, is not appreciative of the fainter light approaching the minimum, the visible diameter of the central disk is somewhat less. It is equal to the diameter of the cone in the plane of farthest descent of vision, as indicated by the dotted line in Fig. 84, and this will depend on the brightness of the star observed. In the case of a very bright star, the greater size of the visible disk and irradiation on the retina caused by a brilliant light source together make such a star appear to be considerably larger than a faint one. The image of a very faint star appears considerably smaller, the feeble illumination giving the impression that the image is a mere point.
The linear diameter in the focal plane of the first bright ring (second maximum) is d=l.62 y F/r.
Resolving Power
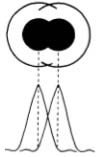
The angular diameter of the first minimum, aa, in the focal plane is equal to 11/A seconds of arc, where A is the aperture of the telescope in inches. It is thus an inverse function of the diameter of the mirror, and leads to a determination of the ability of the telescope to resolve detail. Theoretically, two adjacent points can be seen as separate when the center of the diffraction disk of one falls on the first minimum of the other, that is, when the separation of the centers of the disks is not less than the semi-diameter of the first minimum, or 5.5/A. For a 6-inch telescope, this is about 0.92 seconds of arc. But, as has been shown by W. R. Dawes, a noted 19th-century observer of double stars, the least angular separation of two stars that can be seen as double is somewhat less (Fig. 85), and is given as Dawes’ limit, a in the following formula:
a = 4.56/4.
This establishes 0.76 seconds of arc as the minimum separable angle, for points equally bright, in a 6-inch telescope.
With double stars of this order of separation, a considerable amount of magnification must be employed to enlarge the angle sufficiently for the eye to define the separate disks, presumably to the minimum angle that can just be resolved by the eye.
The resolving power of the eye, or visual acuity, is the angle at the eye of twoadjacent points of equal brightness that can just be resolved, and below which no distinguishable difference in dimension is apparent, ihe minimum angle is taken to be about 1 minute of arc with a pupil diameter of 4 mm., although acuity is fairly constant for pupillary openings between 2 mm. and 5 mm. Below 2 mm. there is a rapid decline due to the increasing size of the diffraction pattern on the retina; above 5 mm. chromatic and spherical aberration of the eye effect a decrease in acuity.
For most eyes, 1 minute of arc also seems to be the limit in comparing objects of different widths. Objects of a much smaller angular size may be easily seen, however. The limit of visibility is a matter of contrast, as in the case of a fine wire stretched across a background of cloudy sky, which wire may still be visible when its angular size is only 1/50 of a minute. For objects placed against a dark background, as in the case of the stars, there is almost no limit.
But although the theoretical resolving power of the eye is usually taken to be 1 minute of arc, as stated above, experiments by the author with a group of students indicate that the eye does not actually perform down to this limit with separate luminous points. Pinhole perforations of the order of 0.0003″ in diameter were made in pairs in the painted surfaces of glass slides, so that at 10″, the distance of best vision, their angular separations ranged from 1 to 4 minutes. Conditions were such as to provide a pupil opening of about 4 mm. Where there was more than a slight difference in pinhole diameter or brightness, resolution was limited to from 2½ to 4 minutes of arc, but with equal pinholes, and moderate illumination, several students were able to resolve a 2-minute separation. Only one student succeeded in resolving an equal pair of 1½-minute separation. As is theoretically to be expected, resolution deteriorated with brilliant illumination of the pinholes, and with unequal components.
It is rather well known that only a very keen eye can separate the wide components of Epsilon Lyrae, of magnitudes about 4 and 5, and 3½ minutes of arc apart. The inequality in brightness of the components is partially responsible for the difficulty of resolution, and the lack of stability in the atmosphere is also a factor. A more liberal value than the 1-minute minimum must therefore be taken for use with the telescope, and in practice 4 minutes of arc has been found to be about correct. For a 6-inch telescope, then, to reveal as double two nearly equal stars separated by 0.76 seconds of arc, a magnification of 316, a little better than 50 per inch of aperture, must be employed.
With the f/8, so high a power is not generally apt to be used, due to the difficulty of acquiring an eyepiece of the requisite focal length. Occasionally, however, one is able to pick up an eyepiece with a focal length of 1/6″ or even l/8″. But if the atmosphere is tranquil enough and the mirror is well figured, a pretty close approach to Dawes’ limit can be expected with a power of about 200. To resolve detail in an extended object such as a planet, the least magnification is one that will make the diffraction disk just visible to the eye; in other words, magnification that will enlarge the disk to an apparent angular diameter of 1 minute. This is found to be about 78x for a 6-inch mirror, or 13 per inch of aperture for any telescope. But the effort to detect detail at the limit of resolution imposes a severe strain on the eye, so some additional magnification must be used. For lunar, planetary, and terrestrial observations, probably up to four times this amount may be usefully applied, but further magnification will actually result in a loss of definition, because of the visibility of the separate diffraction patterns. A vivid demonstration of this can be made by trying the diaphragm shown in Fig. 87 on the planet Jupiter, for example, on a quiet night, first with a 1/2″ eyepiece, and then with a 1/4″, and comparing the results. Except for the separation of close double stars, no benefit is to be derived from magnifications in excess of about 50 per inch of aperture.
Diffraction from Obstructions
The effect of obstruction by the vanes or spider legs supporting the secondary is to interrupt the continuity of the diffraction rings, the scattered light brightening the arcs adjacent to the interruptions. The visible effect is the ray-like radiation fanning out from a bright star image. Each vane causes a complementary ray to be formed on the opposite side, so that if the diagonal is supported by three vanes, six rays will be seen. With a four-legged spider, the complementaries coincide with the original diffraction, and only four rays result. Increasing the thickness of the vanes increases the amount of diffracted light. In photography, the rays are often useful, as they make it possible to locate exactly the center of a star image which, due to long exposure, may be of enormous size on the plate.
The effect of the central obstruction is to reduce the size of the Airy disk, and to scatter more light throughout the pattern, at the expense of the intensity in the central disk; additional diffraction rings may thereby be made visible around a star image. When a 3″ stop was tried on Vega, the central disk shrank almost to a point, and numerous rings appeared. It was quite evident that there was a substantial increase in the amount of scattered light. Diffraction effects are more pronounced when a square stop, such as one in the shape of the obstruction from a rectangular diagonal, is used, although diffraction is kept at a minimum when the corners are made to coincide with the vanes, as in Fig. 63. In any other position, the corners create four additional rays radiating from the bright star image. The practice sometimes followed of reducing the area of the obstruction by cutting off the corners of the rectangular diagonal is not a wise one, as additional diffraction is introduced by each additional corner.
It has been found that the scattering of light, which impairs contrast, definition, and resolving power, becomes conspicuous when the area of the central obstruction exceeds six per cent of that of the mirror. Thus, in order to keep the diffraction from this cause within tolerable limits, the minor axis of an elliptical diagonal should not be greater than approximately one fourth the diameter of the primary mirror.