In order that the maximum benefit may be derived from its use, the permanently mounted telescope should be in accurate equatorial adjustment and equipped with setting circles. When the circles are finally adjusted and fixed, the telescope can then be set to the known declination and hour angle of a celestial object, and it will be found to be in the field of view. The hour angle is the difference in time between the hour circle of the object and the observer’s meridian; in other words, it is the difference between the right ascensions of the object and the observer’s meridian. The right ascension of the meridian is always equal to the local sidereal time. An example of how to convert local civil time (LCT) to local sidereal time (LST) will follow shortly.
Making the Circles
A ready way of procuring the setting circles is to purchase two cardboard protractors 6″ in diameter. These come accurately engraved on Bristol board, with each quadrant marked from 0° to 90°, and graduated to half degrees, which is as much accuracy as the amateur astronomer will generally have use for. The* protractors can be cut out and glued to plywood disks having accurately bored-out centers, varnished, and slipped over any convenient parts of the mounting. Pointers or indicators must likewise be attached. It is best to have the pointers attached to a stationary part of the mounting, while the circles rotate with the axes. The method of numbering on the protractors is ideally suited for the declination circle, but an alteration will have to be made for the hour circle. Change each quadrant so that, instead of containing nine major divisions of 10° each, it will be divided into six divisions reading from Q hours to 6 hours, each 1° division then being equal to four minutes of time. The hours will be read in either direction starting at 0 hours.
The cardboard circles will render good service for a time if protected from the weather, but the construction of a more permanent set should be attempted while you are learning how to use the first ones. Experience with the cardboard circles may prove that half-degree graduations are not necessary.
Lacking the means of mechanically making precise graduations on metal rings or disks, you may transfer the divisions, as accurately as patience will permit, from a protractor or other suitably graduated device onto durable plastic disks. An excellent engraving tool can be made from an old hack-saw blade by grinding a hook-shaped cutter into it close to one end, so that in being drawn across a surface, bearing against a straightedge (just as in using a pencil), a clean groove will be cut. The hook edge is ground on the corner of a grinding wheel, and that part of the blade is also thinned down against the wheel until it is 0.008″ or 0.010″ thick, so that grooves of similar width will be cut. If this is carefully done, with the lines cut a few thousandths of an inch wide and deep, and filled with a contrasting color of paint or sealing wax, the circles will be both neat and serviceable. Sealing wax can be dissolved in wood alcohol, rubbed into the grooves with the fingers, and the surplus scraped off of the surface with the straight edge of a stiff piece of paper, such as a business card.
Adjustment of the Tube
It is assumed that the polar and declination axes of the mounting are perpendicular to each other. The mirror’s axis, presumably coincident with the axis of the tube, must now be brought perpendicular to the declination axis. Place both declination axis and tube in a horizontal plane, and clamp the polar axis. Position the tube by rotating it in its saddle so that the eyepiece adapter tube is parallel to the ground. Plant two stakes in the ground exactly in line with the center of the tube and on opposite sides, each about 200 feet distant. If this much room is not available, use of a longer adapter tube to hold the eyepiece may enable you to bring the stakes into focus even though they are closer. The stakes should be plumb in the line of sight. Look into the low-power eyepiece, and the first stake should be seen in the field of view. Swing the tube on the declination axis through 180°, and the other stake should be seen in the field. By appropriate shimming at either end of the saddle, both stakes must be brought exactly to the center of the field. A high-power eyepiece should be used for a final determination. Watch out for warping of the wooden saddle after these adjustments are made.
If sufficient ground space is not available for the above test, defer alignment of the mirrors until the mounting is built, and use the empty tube, fitted with cardboard disks at each end, one disk having a 1/16″ centered peephole, and the other a l/2″ central aperture. This will provide a field of view of a little more than 1/2°. Plant the stakes as far off as possible, or better still, suspend plumb lines. Sighting through the peephole at first one and then the other plumb line, bring them both to the center of the 1/2″ aperture by shimming as described.
Adjustment of the Polar Axis
At the present time, Polaris is almost exactly 1 from the celestial pole and describes a diurnal circle of that radius about it. Twice in each 24 hours, therefore, at upper and lower culmination, the star is exactly north. And twice daily, at eastern and western elongation, it is at exactly the same altitude as the celestial pole. We shall first aim the polar axis true north, and later make the adjustment for latitude (altitude of the pole). Let us suppose that we are ready to begin the adjustments on the evening of May 17, 1947. The telescope is located in latitude 40 52′.0 north, and longitude 73 46′.2 (4h 55m 4s.8) west. Our watch is set by radio time signal to Eastern standard time (EST), one hour slower than daylight saving time, and five hours slower than Greenwich civil time (GCT), which is also called Universal time (UT). (Other time zone corrections in the United States are: Central, standard, six hours slower than GCT; Mountain standard, seven hours; Pacific standard, eight hours.)
No amateur observer can plan observations of celestial bodies without the aid of either the American Nautical Almanac (price about $2.00) or the American Ephemeris and Nautical Almanac (price about $4.00), published annually and for sale by the Superintendent of Documents, U. S. Government Printing Office, Washington 25, D. C. The arrangement of these publications is the same each year, so it will be easy for the reader to follow the calculations in this discussion (which have been made using the 1947 Ephemeris), and to make approximate substitution.
From page 550 of the 1947 Ephemeris, take out the following data on Polaris’ culmination:
| May 20, GCT, upper culmination |
9″ |
56′” |
45s |
| Variation in 3 days |
+ 11 |
45.3 |
|
| May 17, GCT |
10 |
08 |
30.3 |
| Longitude correction, 41′ 55′”. 1 |
– 48.2 |
||
| May 17, LCT, upper culmination |
10 |
07 |
42.1 |
| Correction to standard time |
– 04 |
55.2 |
|
| May 17, EST, upper culmination |
10 |
02 |
46.9 |
| 12 hours less lm 57S.6 |
11 |
58 |
02.4 |
| May 17, EST, lower culmination |
22 |
00 |
49.3 |
As stated in the instructions with the table, the time, 9h 56m 45s, of the transit at Greenwich on May 20th must be corrected for three days, using the variation per day given as 3m 55s.1, giving us the Greenwich transit on May 17th. The variation per day is positive because the 17th precedes the 20th. Events happen slightly later because of our longitude 4h 55m.l west of Greenwich, requiring the slight correction of 4.92 times the variation per hour of 9.80 seconds. The result is the time of culmination at our local meridian in local civil time, whereas our watch is set for the time of the 75th meridian. We are 4m 55s.2 east of that meridian, so must correct our time by subtracting this amount. (The choice of a longitude produces a similarity of numbers which should not be confused with each other. The 4h 55m.l represents our distance west of Greenwich, and 4m 55s.2 our distance east of the 75th meridian on which Eastern standard time is based.)
The result shows us that at 10:02:46.9 on the morning of May 17th Polaris will transit our upper meridian, reaching upper culmination during the daylight hours. We shall obviously have to use lower culmination, which the same table tells us will occur 12 hours later, diminished by half the numerical value of the variation per day. Therefore, at 10:00:49.3 p.m. May 17th, Polaris will cross the meridian below the pole.
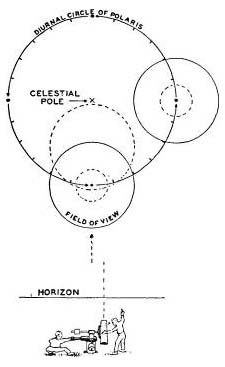
So at about 9:30 that evening, we set the declination axis in a horizontal position and clamp the polar axis. We point the telescope northward and sweep in a vertical plane, in order to pick up Polaris, which must be brought to the center of the field by rotating the wye fitting east or west on the pier (Fig. 83). We try, as nearly as possible, to accomplish this by 10:00 p.m. Set the hour circle so that the pointer is on zero, and note the reading on the declination circle. Release the polar axis and turn it through 180° by the hour circle, so that the declination axis is again horizontal, with the telescope on the other side of the pier. Clamp the polar axis, and bring Polaris to the center of the field by sweeping in a vertical plane as before. Again note the reading on the declination circle. It is not likely that both of the readings will be the same. Now move the tube so that the declination pointer just splits the difference between the two readings, clamp it, and bring Polaris to the center of the field by tilting the mount up or down by means of the north-south lock nuts on the pier. For better accuracy, the adjustments should be completed with a high-power eyepiece. Because of Polaris’ nearness to the pole, its diurnal motion across the line of sight is slow (see caption in Fig. 83), and for completion of these preliminary adjustments a period of 20 minutes —10 minutes before and 10 minutes after the moments of culmination and elongation—may be allowed. This will not affect the final results, since the observations will have to be repeated anyway.
The polar axis now points to Polaris, which, within the interval just mentioned, is substantially due north and 1° below the pole. A partial correction for altitude may be made by raising and lowering, respectively, the north and south lock nuts, tilting the polar axis upwards, so that Polaris is brought to the upper edge of the inverted field (large dotted circle, Fig. 83, inverted).
At nearly four o’clock the next morning, Polaris will be at eastern elongation, and we may indulge in a short nap, but the time of the elongation should be previously determined. The upper culmination that morning will occur at 9:58:51.8, and the last column of the Polaris table we have been using shows that at our latitude elongation occurs 5h 55m.6 earlier. Therefore, the eastern elongation is at 4:03:15.8 on the morning of May 18th.
At about 3:30 a.m., we begin working again, setting the telescope as in Fig. 72, with the declination axis in a vertical plane and with the tube above the pier. Clamp the polar axis, and bring Polaris to the center of the field by continuing the adjustment of the north-south lock nuts. Finish up as nearly as possible to the 4:03 position of Polaris, and set the declination circle to read 89°.
On the following night, May 18th, we shall want to check the adjustments on another star, preferably one near the celestial equator. The choice of a star can be made by referring to the table on the meridian transit of stars in the Nautical Almanac or by paging through the tables on the apparent places of the stars in the Ephemeris. The simplest way is just to observe the evening sky at this season, whence it is seen that the Ist-magnitude star Spica, Alpha Virginis, is a good choice, and will transit about 9:30 in the evening, an hour before which time it is sufficiently dark to begin.
Choosing 8:30 p.m., May 18th, as our time for starting to work, we compute the meridian angle (negative hour angle) of Spica for that time. This will give its distance east of the meridian and enable us to predict easily the time it will cross the meridian. The methods employed are several, and well known to navigators. If the Nautical Almanac is used, the problem is simply to take out of the star tables the Greenwich hour angle (GHA) of Spica for May 19th at 1:30 Greenwich time. This value, subtracted from our longitude, tells how far Spica is east of our meridian. The Greenwich hour angle is found to be 57° 46′.7, and the meridian angle is 15° 59′.5.
The telescope maker, however, will do well to use the method whereby the local sidereal time is first computed (unless a timepiece running on sidereal time is available), and then the star’s right ascension is subtracted from the sidereal time to give the hour angle. If the answer is negative, the star is east of the meridian an amount called the meridian angle, as already mentioned.
The last column on page 8 and Table III, in the Ephemeris, are use’d. Spica’s position is given on page 299 as R.A. 13h 22m 25s.O, Dec. -10° 53′.3.
| Sidereal time 0h GCT, May 18 |
15h |
39m |
20s.1 |
| 20h 30m May 18 |
30 |
||
| Correction for 20h 30m |
20 |
+ 03 |
22.1 |
| Longitude correction, 4h 55m.l |
+48.5 |
||
| Sidereal time 8:30 p.m. LCT |
20 |
13 |
31.1 |
| Correction standard time (sidereal interval) |
04 |
56.0 |
|
| Sidereal time 8:30 p.m. EST 12 |
12 |
18 |
27.1 |
The difference between this sidereal time and Spica’s tabulated right ascension gives us a meridian angle of lh 03m 57S.9, so that Spica should transit 1 hour and 4 minutes after 8:30, or 9:34 p.m.
Now aim the telescope so that the pointers read 11° south on the declination circle, and lh 04m east of the meridian on the hour circle, and see if Spica is in the field at 8:30. Rotate the mount east or west on the wye to bring the star to a middle division of the field of view, while following it to culmination. At the moment of transit, 9:34 p.m., the hour circle is set to read 0 hours, and the mount is tilted up or down to bring the star to the center of the field. The declination circle is then set to 11° south.
Repeat the observations of Polaris on another evening, and again on a third star, one that is two or three hours east of the meridian. With patience, and if the mounting has been well built, it will be possible to bring the adjustments within the accuracy of the graduated circles.
Where possible, avoid stars having an altitude of less than 20°, as errors due to atmospheric refraction then become considerable, and must be taken into account. Therefore, those amateurs residing in low latitudes should apply a correction for refraction when making adjustments by Polaris. This correction, to be subtracted from the observed altitude of a star, can be taken from Table A in the Nautical Almanac.
Sidereal Time from the Stars
When the adjustments have finally been completed, sidereal time can be found without computation by observing the transit of any celestial object, the right ascension of which is known. Its right ascension is, at the moment of transit, equal to the local sidereal time. Or, at any time, center the object in the field of view, and note the hour angle as read by the indicator. Adding this to or subtracting it from the right ascension of the object, depending on whether it is west or east of the meridian, will give the local sidereal time.
It will be found more convenient, however, to set a spare timepiece, and to keep it running on sidereal time on nights of observation. The slight difference in the rate of an ordinary watch will not matter during one night’s use. Observatory clocks run at the sidereal rate, making computations unnecessary. Amateurs may purchase sidereal watches and clocks from a few American manufacturers.
The Nautical Almanac and the Ephemeris explain the method of finding sidereal time, but for a more complete study of the various kinds of time, the reader is advised to consult a standard astronomy or navigation textbook.
Locating True North by the Sun
To find the watch time of meridian transit of the sun, in ‘order to locate true north by day, we must know the exact longitude. This can be found with’ sufficient accuracy from maps of the U. S. Coast and Geodetic Survey. The equation of time, that difference between the sun and the clock which is caused by the ellipticity and inclination of the earth’s orbit (as referred to the equator), is taken from the Nautical Almanac or the Ephemeris for the date and hour of Greenwich time, and applied with its sign reversed. Noon at any place occurs at 12:00 local apparent time.
For example, use page 8 of the Ephemeris to find the watch time of transit of the sun on May 18, 1947, at a place in longitude 73° 46′.2 west:
| Local apparent time of local apparent noon (LAN) |
12h |
00m |
00ss’ |
| Equation of time, 17:00 GCT |
11 |
03 |
42 |
| LCT of LAN |
20 |
56 |
18 |
| Correction to standard time |
04 |
55 |
|
| Watch time, LAN |
20 |
51 |
23 |
Set up a plumb line over the pier, and mark the direction of its shadow at the moment of local apparent noon. This will be a true north-south line. The watch will, of course, have been accurately set by radio time signal.